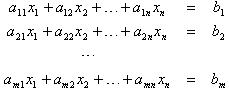Kulcsszó

Meghatározás

algebrai aldetermináns

Az A mátrix a_ij eleméhez tartozó aldeterminánst úgy kapjuk meg, hogy vesszük az A_nxn mátrix i. sorának és j. oszlopának elhagyásával keletkező (n-1)x(n-1)-es mátrix determinánsát; az aldetermináns attól algebrai, hogy azt még beszorozzuk (-1)^i+j -nel, vagyis akkor kell előjelet váltani, amikor az i+j index-összeg páratlan.

Cramer-szabály

A Cramer-szabály kizárólag a lineáris egyenletrendszer egyértelmű megoldásának kiszámítására alkalmas.

Az x ismeretlen-vektor j. koordinátáját úgy kapjuk meg, hogy az A együttható-mátrixban a j. oszlopot kicseréljük a jobb oldali b vektorra, vesszük az így kapott mátrix determinánsát, majd elosztjuk az eredeti A determinánsával.

( j=1,2...n )

determináns

Az A négyzetes mátrixnak a determinánsa a detA vagy az jelölésű valós szám, melyet úgy kapunk, hogy a mátrix tetszőlegesen kiválasztott sorának (vagy oszlopának) elemeit a hozzájuk tartozó algebrai aldeterminánssal megszorozzuk, majd a szorzatokat összeadjuk.

egyenletrendszer egyértelmű megoldásának feltétele

Az A*x = b egyenletrendszernek akkor és csak akkor van egyértelmű megoldása, ha a detA nullánál különböző (detA≠0). Máshogy: a mátrixot alkotó oszlopvektorok (vagy sorvektorok) lineárisan függetlenek.

egyenletrendszer mátrix-alakja

A*x = b, ahol

egységmátrix

A négyzet alakú mátrixok egy speciális fajtája, melyben a főátlóban állnak csak 1-esek, máshol pedig 0-k.

Általánosan E az nxn-es egységmátrix.

együttható-mátrix

Az A*x = b lineáris egyenletrendszer A mátrixa

ekvivalens átalakítások

Az ekvivalens átalakítások alkalmazásával az egyenletrendszer nem változik a tartalmát és a megoldását illetően:

• az egyenletek sorrendje felcserélhető;
• az egyenlet 2 oldalát beszorozhatjuk ugyanazzal a nem nulla számmal;

az egyik egyenlethez hozzáadhatjuk egy másik egyenlet k-szorosát.

elem

A számtáblázat adott cellájában elhelyezkedő adat, melynek azonosítása a számtáblázat nevével és sor-oszlop indexeléssel történik.

érték

Az adat aktuális állapota.

fa

Az összefüggő körmentes gráf a fa; speciális irányítással az ún. gyökeres fa. A fában egy kitüntetett pont a gyökér, melyen kívül az összes többi pontnak (utódnak) van megelőzője (szülője), ami a gyökérből a pontba vezető körmentes útban a pontot megelőző pont.

Gauss-elimináció módszere

Az ismeretlenek kiszámítása céljából az egyenletekből sorban kiküszöböljük az ismeretleneket, hogy végül n darab egyismeretlenes egyenletet kapjunk az egyes ismeretlenekre.

A Gauss-elimináció menete mátrix-alakban:

1. A*x=b helyett vegyük csak az A együttható-mátrix b-vel történő kibővítését: , melyet
2. az ekvivalens átalakítások segítségével felsőháromszög-formára hozunk (melyben a főátló alatt csupa 0 áll),
3. majd átló-formájúra alakítunk (melyben már a főátló felett is 0-k állnak),
4. végül egységmátrix formára hozunk, hogy a jobb oldal a következetes alakításokkal végül már a megoldás-vektort tartalmazza

gráf

A gráf bizonyos elemek és a köztük fennálló közvetlen kapcsolatok halmaza.

Az elemeket csomópontoknak, a kapcsolatokat pedig éleknek nevezzük, illetve pontokkal és szakaszokkal ábrázoljuk grafikusan.

hálózat

Amikor az él más jellemző(ke)t is képvisel, a gráfot hálózatnak vagy súlyozott gráfnak nevezzük (bár nagyon gyakran mégsem teszünk kivételt). Ilyen jellemző lehet: a költség, munkaóra, távolság, időtartam stb., de általánosan azt az él hosszának nevezzük.

határozatlan érték

Az adat aktuális állapota ismeretlen, az értéke nem kitöltött.

homogén egyenletrendszer

Az A*x = 0 lineáris egyenletrendszer.

inverz-mátrix

Az A_nxn mátrix inverze egy szintén nxn típusú mátrix lehet, amelyre igaz, hogy az A mátrixszal bármely oldalról összeszorozva az egységmátrixot adja.

Formálisan: A_{nxn *} A^-1_{nxn =} A^-1_{nxn *} A_nxn = E, ahol E az nxn-es egységmátrix.

inverz-mátrix előállítása aldeterminánsok segítségével

ahol A_ij számok az a_ij elemek helyébe írt algebrai aldeterminánsok

inverz-mátrix kiszámítása Cramer-szabállyal

Amikor Cramer-szabállyal kívánjuk megoldani az n darab egyenletrendszert, akkor az nxn darab determinánst kell előállítani, ami szintén felgyorsítható, ha az új determinánsokat örökké a lecserélt oszlop szerint fejtjük ki, ugyanis a helyére mindig valamelyik egységvektor kerül.

Tehát az

számlálójában a determináns kifejtése éppen az i. oszlopba kerülő j. egységvektor szerint történjen, miután abban mindig egyetlen 1-es és (n-1) darab 0 áll.

inverz-mátrix kiszámítása egyenletrendszerek megoldásával

Az inverz-mátrix definíciója szerint annyi egyenletrendszert kell megoldani, ahány oszlopa van az inverz-mátrixnak. Az összes egyenletrendszer együtthatómátrixa ugyanaz, a jobb oldali konstans-vektorok pedig rendre az egységvektorok.

inverz-mátrix kiszámítása Gauss-módszerrel

A több egyenletrendszer kiszámítása Gauss eliminációval történhet egyszerre, hiszen mindegyikben ugyanazt az A mátrixot kell az ekvivalens átalakításokkal E egységmátrixszá alakítani. Ekkor nem 1, hanem n jobb oldali vektor fog szerepelni a kibővített mátrixban. A szükséges ekvivalens átalakításokat ekkor a vonaltól jobbra több oszlopra is végrehajtjuk. Végezetül az n darab megoldás-vektor az inverz-mátrix oszlopait eredményezi.

Formálisan:

irányított gráf

Ha egy gráfban az élekhez irányítást is rendelünk, irányított gráfot kapunk (a nem szimmetrikus kapcsolatok kifejezésére).

ismeretlen-vektor

Az A*x = b lineáris egyenletrendszer x vektora

konstans-vektor

Az A*x = b lineáris egyenletrendszer b vektora

körút

Körút az olyan út, amelynek a kezdő- és végpontja megegyezik.

legrövidebb út

Egy súlyozott gráfban két pont közötti legrövidebb út az, ahol az élek hosszának összege a lehető legkisebb.

lineáris egyenletrendszer, egyenletrendszer

Az m egyenletből álló n ismeretlenes lineáris egyenletrendszer:

ahol

• az a_ij együttható az i. egyenletben szereplő j. ismeretlen együtthatója,
• o az x_i az i. ismeretlen,
• o a b_j a j. jobb oldali konstans,
• o i=1,2,...n és j=1,2,...m

lineáris függetlenség

Adott vektorok lineárisan akkor függetlenek, ha kizárólag a csupa nullával vett lineáris kombinációjuk állítja elő a nulla-vektort. Máshogy: egyik vektor sem áll elő a többi lineáris kombinációjaként.

lineáris programozási feladat

Alapfeladat: hányat gyártsunk az egyes termékekből a raktáron lévő mennyiségekből gazdálkodva, hogy az árbevétel a lehető legnagyobb legyen?

Legyen x és y a 2 termékből legyártani kívánt darabszám.

Amikor megfogalmazzuk az egyes alkotókra vonatkozó korlátozásokat (mármint, hogy az x és y darabszámú termékhez szükséges alkotók mennyisége ne haladja meg a raktáron lévő mennyiséget), akkor azt is írjuk hozzá, hogy mindkét mennyiség minimum 0 legyen. A korlátozó feltételek mellé aztán leírjuk az árbevétel függvényét, melyet maximalizálni szeretnénk.

mátrix

Adott nxm darab számnak n sorban és m oszlopban történő elrendezését egy nxm típusú mátrixnak nevezzük.

mátrix szorzása számmal

M_nxm tetszőleges típusú mátrix k-val való szorzása egy szintén nxm típusú mátrixot eredményez, melynek minden eleme k*m_ij lesz.

mátrix transzponáltja

Az A_nxm mátrix transzponáltja egy mxn típusú mátrix, melynek az i. sorába és j. oszlopába kerülő elem az eredeti A mátrix a_ji eleme lesz.

mátrixkód

Amikor m hosszúságú digitális jelsorozatok n hosszúságban (m<n) történő továbbítását választjuk valamely zajos csatornán keresztül, akkor egy generáló mátrixszal való szorzással állítjuk elő az eredeti közleményekhez a kódolt közlemény-blokkokat. A mátrixnak m sora van és n oszlopa, hogy balról beszorozva az 1xm-es eredeti jelsorozattal, a kapott 1xn-es kódolt jelsorozatot kapjuk. A G generáló mátrix tetszőleges módon tartalmazhatja a 0-kat és 1-eket, bár szokás az első m oszlopban az egységvektorokat tartani.

A kódolt közlemény-blokkot tehát a következőképpen kapjuk meg: b = a×G.

A műveletvégzés a kettes számrendszerben és tagonként külön történik (tehát: 1+1=0 mod2).

A küldött 2^m-féle jelsorozat helyett a vett jelsorozat viszont 2ⁿ-féle lehet, azaz többször annyi jelsorozatról kell majd valamilyen módon eldönteni, mint ahányat elküldtek, hogy mi lehetett a ténylegesen elküldött jelsorozat.

mátrixok összege

Az A_nxm + B_nxm összeg egy szintén nxm típusú mátrixot eredményez, melynek minden eleme az ugyanolyan helyen álló A- és B-beli elemek összege (a_ij+b_ij ).

mátrixok szorzata

Az A_nxk * B_kxm szorzat egy nxm típusú mátrixot eredményez, melynek az i. sorában és j. oszlopában lévő elemét úgy kapjuk meg, hogy az A mátrix i. sorvektorát a B mátrix j. oszlopvektorával skalárisan összeszorozzuk. (Formálisan a k-ra összegezve:
∑ a_ik * b_kj.)

minimális fa

Az egyik adott pontból az összes többi pontba tartó legrövidebb utak fája egy súlyozott gráfban.

n-edfokú polinom

A n-edfokú polinom (valójában hatványfüggvény) általános alakja:

Az n-edfokú polinomnak n+1 darab paramétere van (ezek az a_i együtthatók, i=0,1, ..., n)

nulla-mátrix

Bármely típusból az olyan mátrix, melynek minden eleme 0.

összefüggő gráf

Összefüggő a gráf, ha bármely két pontja között van út.

számtáblázat

Adott számú sorba és adott számú oszlopba elhelyezett számok táblázata.

út

Két pontot összekötő út a kezdőpontból a végpontba tartó, egymáshoz csatlakozó élek sorozata, mely egyetlen ponton sem megy át kétszer.