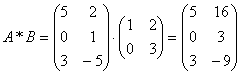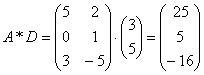Emlékezzünk vissza a vektor koordinátákkal történő megadására! Például a fenti C és D mátrix valójában három- illetve kétdimenziós vektor, a középiskolában c és d, esetleg c és d volt a jele. Ha egy vektort a háromszorosára kívántunk nyújtani, akkor annak minden koordinátáját beszoroztuk hárommal. Pl. 3*(2, 4, 0)= (6, 12, 0)

A mátrixok esetében is így történik a számmal (skalárral) való szorzás.

M_nxm tetszőleges típusú mátrix k-val való szorzása egy szintén nxm típusú mátrixot eredményez, melynek minden eleme k*m_ij lesz.

Például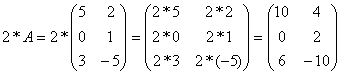

Két mátrix csak akkor adható össze, ha azonos a típusuk. A fenti A mátrix a fenti B-vel nem adható össze. Hasonlóan, mint a vektoroknál; csak ugyanolyan dimenziójú vektorokat adhattunk össze, mégpedig koordinátánként végezve el az összegzést: (1, 2, 1)+(4, 0, 0)=(5, 2, 1)

Általánosan az A_nxm + B_nxm összeg egy szintén nxm típusú mátrixot eredményez, melynek minden eleme az ugyanolyan helyen álló A- és B-beli elemek összege (a_ij+b_ij ).

Példa két 3x2-es mátrix összegére:

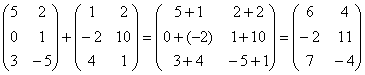
Legalább példákon keresztül ellenőrizzük, hogy bármely A mátrixhoz az ugyanolyan típusú nulla-mátrixot hozzáadva, az eredeti mátrixot kapjuk vissza!

A+O=A

Miután az összeadás a számok körében felcserélhető művelet (azaz x+y=y+x), könnyen belátható, hogy a mátrixok összeadása is az.

A+B=B+A

Amikor két mátrix szorzásáról beszélünk, már nem ennyire egyszerű a dolgunk. Amikor két azonos dimenziójú vektort skalárisan szoroztunk össze, akkor az eredmény skalár, azaz szám, és nem vektor lett. Például a termékekhez tartozó megrendelt mennyiségek vektorát skalárisan kell összeszorozni az egyes termékek egységárából képzett vektorral ahhoz, hogy kiszámítsuk az árbevételt:

(12, 20, 3)*(10, 20, 50)= 12*10+20*20+3*50=670

Az egyes koordináták szorzatát végül összegeztük, így kaptunk egy számot, azaz skalárt.

Mondjuk ki végre, hogy valójában egy többsoros mátrix több sorvektorból, illetve a többoszlopos mátrix több oszlopvektorból áll!

A bevezető példa alapján próbáljuk megválaszolni, mennyit fognak fizetni az egyes partnerek a szállításért, ha az A_i áruk egységárának vektora most is (10, 20, 50) valamilyen pénzegységben!

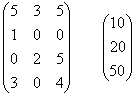
A szállított mennyiségek mátrixának első sora az első partner sorvektora, amit az egységárak vektorával skalárisan összeszorozva éppen az első partner által fizetendő összeget kapjuk: 5*10+3*20+5*50=360

Természetesnek tartjuk, hogy a szorzatban részt vevő vektorok koordinátái ugyanannyian vannak, és minden összeszorzott koordináta-pár ugyanannak az árunak a jellemzője (a mennyiség és az egységár).

A szállított mennyiségek mátrixa 4 sorvektorból áll, melyekre rendre elvégezve a skaláris szorzást ugyanazzal az árvektorral, az egyes partnerek által fizetendő ősszegek vektorát kapjuk.

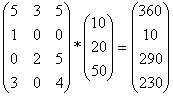
Amint több szállító vesz részt a szállításban különböző árakkal, többféle fizetendő összeget is képezhetnénk. Legyen még egy szállító, melynek ugyanerre a 3 árura más, például (20, 20, 40) lenne az árvektora! Számítsuk ki, hogy az egyes partnerek mennyit fizetnének az egyik és mennyit a másik szállítónak!

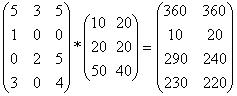
Az előzőhöz képest ugyebár nem 1, hanem 2 oszlopvektor a válasz, melynek a koordinátái rendre az egyes partnerek által fizetendő összegeket mutatják.

A bemutató letöltése.

Általánosan az A_nxk * B_kxm szorzat egy nxm típusú mátrixot eredményez, melynek az i. sorában és j. oszlopában lévő elemét úgy kapjuk meg, hogy az A mátrix i. sorvektorát a B mátrix j. oszlopvektorával skalárisan összeszorozzuk (formálisan a k-ra összegezve: ∑ a_ik * b_kj ).

Nincs definiálva az olyan szorzat, ahol a bal oldali mátrix oszlopainak száma nem egyezik meg a jobb oldali mátrix sorainak számával.

Ellenőrizzük, hogy egy tetszőleges A mátrixot az alkalmas egységmátrixszal bármely oldalról összeszorozva visszakapjuk az eredeti mátrixot!

A*E = E*A = A

Részletesebben: A_nxm *E_mxm= E_nxn *A_nxm=A_nxm

Ha viszont a fenti A mátrixban felcserélnénk a sorokat az oszlopokkal, akkor az alábbi 2x3-as mátrixot kapnánk:

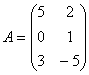
, jelölése lehet T vagy t az A kalapjában.

Általánosan az A_nxm mátrix transzponáltja egy mxn típusú mátrix lesz, melynek az i. sorába és j. oszlopába kerülő elem az eredeti A_ji eleme lesz.

Kizárólag a négyzetes mátrixok estében nevezhetjük ezt a műveletet a főátlóra való tükrözésnek.

Végül tisztázzuk, hogy egy mátrix n. hatványát úgy kaphatjuk meg, hogy a mátrixot önmagával n-szer összeszorozzuk. Ennek persze az a feltétele, hogy a mátrixnak annyi sora legyen, mint oszlopa.

Az összeadás ellentett művelete - akárcsak az algebrában - a kivonás lesz, bár az alapműveletekből gazdálkodva helyesen azt mondanánk, hogy elegendő az A (-1)-szeresét hozzáadni az A-hoz, hogy megkapjuk a nulla-mátrixot. Természetesen ez valóban az elemek közötti kivonást jelenti.

Ahogy az algebrából tudjuk, az a nem 0 valós számnak van a szorzásra nézve is ellentettje: az 1/a, azaz az a^-1. Azért ez, mert az adott számot csak ezzel az inverzével összeszorozva kapjuk meg az egységelemet (a*a^-1=1). A mátrixok közül sem bármelyiknek lesz inverze, de ha lesz, akkor annak az a dolga, hogy kielégítsen egy ugyanilyen összefüggést: A*A^-1=E. (A mátrixok esetében sem a mátrix reciproka, sem az osztás művelete nem használatos elnevezés.) Később tisztázzuk az inverz létezésének feltételét és a kiszámítás módját.