Mivel a középiskolában előforduló polinomoknak, a racionális törtfüggvényeknek, a trigonometrikus, az exponenciális és logaritmus-függvényeknek több intervallumból álló értelmezési tartomány fölött is intervallumonként egyetlen darabból állt a grafikonja, nem hangoztattuk, hogy azok folytonosak. A folytonosság definiálása ugyanis nem megy a határérték fogalma nélkül - ami viszont főiskolai követelmény.

Jelen képzésben csak próbáljuk meg az egyszerűbb függvények menetének felvázolása alapján kiolvasni a szakadás megjelenését, hogy megértsük: abban a pontban nem folytonos a függvény, amelyben szakadása van.

Az előjel-függvény, vagy az egészrész-függvény grafikonján jól látjuk, hogy valamely pont(ok)ban ugrik, azaz „nem halad simán" a függvény.

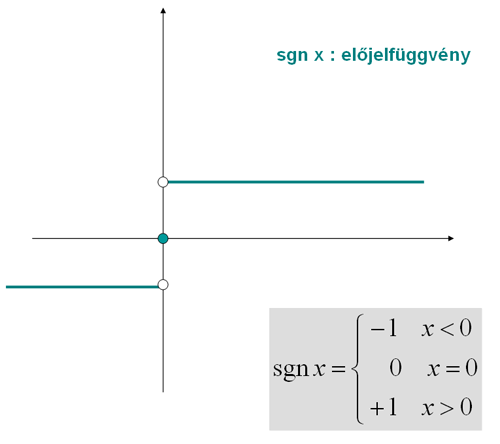
Az függvénynek ún. hézagpontja van az x=2-ben, hiszen 0/0, azaz határozatlan benne a helyettesítési érték. A függvény valójában az x+2 egyenes egy lyukkal az x=2 helyen, mert abban nincs értelmezve. A függvény 2 darabja viszont az x=2-ben „össze akar érni", azaz megszüntethető szakadással rendelkezik. Valójában jobbról és balról haladva x szerint a 2 felé, a függvényértékek ugyanoda, az y=4-be tartanak.

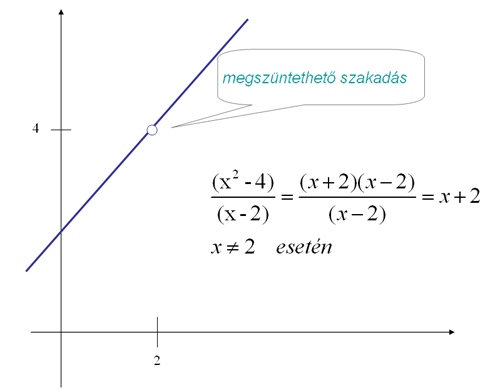
Csak ösztönzés céljából jegyzem meg ezen a képzésen, hogy a függvény - ami fontos a rezgések fizikájában - nem ábrázolható holmi érték-táblázat segítségével, és ezért nem állítható teljes bizonyossággal, hogy annak a 0 pontban megszüntethető szakadása lenne. A határérték-számítás alapján viszont a függvény 2 darabja a 0 pontban ugyanazt az 1-et akarja felvenni, magyarul azt mondanánk, hogy a sík (0,1) pontjában „össze akar érni".

A függvénynek a 0-ban van határértéke, tehát akár az egész számegyenes felett folytonos függvénnyé tehető a következő definícióval:

f(x)=

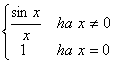
Tudományosan: a függvény az értelmezési tartomány x=p pontjában akkor folytonos, amikor a p pontbeli határértéke megegyezik a helyettesítési értékével. Egy intervallum fölött pedig akkor folytonos, ha annak minden pontjában az.

A sorozat határérték fogalmának az egyik jelentősége éppen a valós függvény pontbeli határértékének meghatározásában van. Ha például az összes x=p pontba tartó sorozat esetén a függvényértékek sorozata is konvergens lenne, akkor a valós függvénynek az x=p pontban lenne határértéke. Ez a definíció csak a függvény ábrázolása mellett használható ki.