7.2. Függvényvizsgálat
Bizonyítható, hogy tetszőleges függvény 1. deriváltjának előjele az eredeti függvény monotonitásáról ad információt, a 2. derivált előjele pedig az eredeti függvény hajlékonyságáról (görbületi irányáról).
Formálisan:
Ahol f'(x)>0, ott f(x) szigorúan monoton nő;ahol f'(x)<0, ott f(x) szigorúan monoton csökken.
Ahol f''(x)>0, ott f(x) konvex;
ahol f''(x)<0, ott f(x) konkáv.
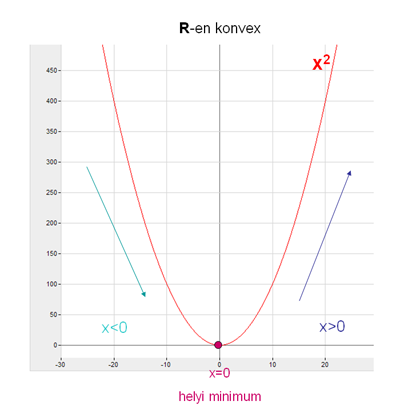
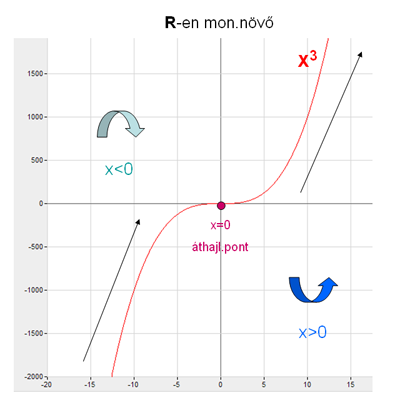
Nézzük csak a standard parabola és az 'x-a-harmadikon' grafikonját!
Újabb hasznos tételek:
Ha az f(x) függvénynek az x0 (x0
Df) helyi szélsőérték-helye, akkor f'(x0)=0.
Ha az f(x) függvénynek az x0 (x0
Df) áthajlási pontja, akkor f''(x0)=0.
Figyelem: az előbbi állítások megfordítása nem mindig igaz! E tételek segítségével egy összetett függvény menete is jól vázolható, és közben a helyi szélsőérték-helyek illetve áthajlási pontok is kijönnek. Tetszőleges parabola (ld. grafikon) egyetlen szélsőérték hellyel rendelkezik, mert abban a függvény értelmezve van, és annak monotonitása a pontban megváltozik. A függvény konvexitása nem változik meg sehol, tehát áthajlási pontja nincs.
Az x3 görbe (ld. grafikon) végig monoton nő, tehát lokális szélsőértékhelye nincs, de az x=0 áthajlási pontja, mert azon a helyen konkávból konvexbe hajlik a görbe. A differenciálszámítás egyik alkalmazása tehát a függvény menetének vizsgálatnál van. A gyökkeresés nehézségétől eltekintve így pontos recept szerint haladva mindent megtudunk egy függvényről, és fel tudjuk vázolni a grafikonját (a vázolásnál az y szerinti egység elhagyható, mégis pontos képet kapunk a függvény menetéről).