A derivált fogalmának a bevezetése a meteorológiai ballon g(x) és h(x) folytonos függvényekkel leírt emelkedésének tárgyalásával indult.

A g(x) függvény szerint emelkedő ballon útjának deriváltja: g'(x)=(50+4x)'=4, tehát minden időpontban ugyanaz a pillanatnyi sebessége.

A h(x) függvény szerint emelkedő ballon útjának deriváltja: h'(x)= (20+x²)'=2×x, tehát tetszőleges x időpontban 2x a ballon pillanatnyi sebessége.

Meg kell jegyezni, hogy az egyenes vonalú egyenletes (vagy egyenletesen változó) mozgás esetén a mozgó test útja (itt a ballon útja) valójában az egyenesen való helye valamely kezdőponthoz képest. Az út tehát az iránytól függően negatív is lehetne.

Rajzoljuk fel a 2 derivált-függvényt! 

A fizikából ismeretes, hogy adott idő alatt megtett utat az idő és a sebesség szorzata adja meg. A pillanatnyi sebességet leíró deriváltak most egyenesek, amelyek alatti terület nagyságát kiszámolni nagyon egyszerű, mert még  tetszőleges a és b között is téglalap vagy trapéz alakú területekről van szó.

Figyelem! A terület most sec*m/sec=m, azaz méterben, tehát út-egységben szerepel.

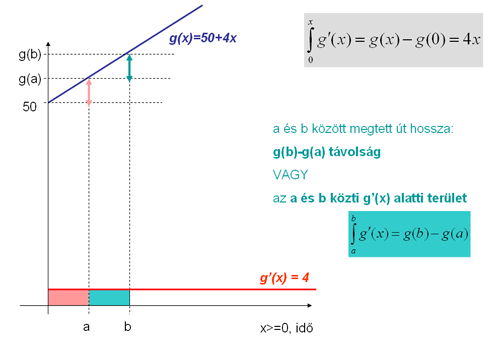
A g(x) minden másodpercben újabb 4 m-t tesz meg, tehát a g'(x) konstans egyenes alatti terület 2 időpont között egy téglalap területeként számolható ki, az időpontok közti távolság és a  konstans 4-es magasság szorzataként.

Azonnal mutatom egy f(x) függvény görbéje alatti terület x=a és x=b egyenesek közé eső darabjának a függvénytanos jelölését:

A h(x) a 0. másodperctől az 1. másodpercig a h'(x) alatti háromszög területének kiszámolásával (1*2/2=) 1 métert, a 2. másodpercig (2*4/2=) 4 métert, az x. másodpercig x*2x/2 métert eredményez, összhangban az eredeti út-függvény függvényértékei szerint értelmezett  megtett út nagyságával: h(x)-h(0)= 20+x²-20 (hiszen a ballon a 0. másodpercben nem 0 méternél lett elengedve).

Ha a 3. és 5. másodperc között megtett útra vagyunk kíváncsiak, akkor egy trapéz területét kell kiszámolnunk: 16 méter.

Ez tehát azt jelenti, hogy a derivált-függvény alatti terület a 0 és x pont között az eredeti függvény x-ben és 0-ban felvett függvényértékeinek különbségét - mint a 0. másodperctől mért x idő alatt ténylegesen megtett utat - adja meg:

Újra megjegyzem: a görbe alatti terület nem feltétlenül út-egységben kapott mérték, mint amikor a függvény jelentése a sebesség. A gyorsulás függvény alatti terület például 2 pont közötti sebesség megváltozását eredményezi, azaz más mérték szerinti nagyságot jelent.