Egy általános folytonos f(x) függvény görbéje alatti terület x=a és x=b egyenesek közé eső darabjának a függvénytanos jelölésére szolgál az alak.

Elnevezése: f(x) határozott integrálja a és b között. Értéke egy szám, amennyiben az létezik. Akárcsak a derivált, úgy a határozott integrál is valamilyen típusú határérték az elmélet szerint. A határozott integrál fogalmának bevezetésére akkor került sor, amikor a tartalom helyére lépett a mérték; mégpedig a „mérhető halmazok" skálájának kiszélesítésével, mint például az intervallumok végtelen sorozatának egyesítésével. Egy görbevonalú trapéz területe szintén jól megközelíthető egyre keskenyebb, a görbe alá vagy fölé rajzolt téglalapok területeinek összegével. (Kultúrtörténetileg éppen a latin szumma kezdőbetűjének megnyújtása szerepel az integrálás jeleként.) Egy nagyon kicsi h szélességű és f(x) magasságú téglalap területe jól közelíti az x és x+h, 2 szomszédos osztó-pont közti görbevonalú területdarabot. A végtelen összeg elméletileg az [a,b] intervallum végtelenül finomodó beosztásával végtelen sok - nem feltétlenül azonos szélességű - téglalap területének az összege-ként áll elő. Ez az összeg egy számként akkor létezik, ha a végtelen összegnek van határértéke.

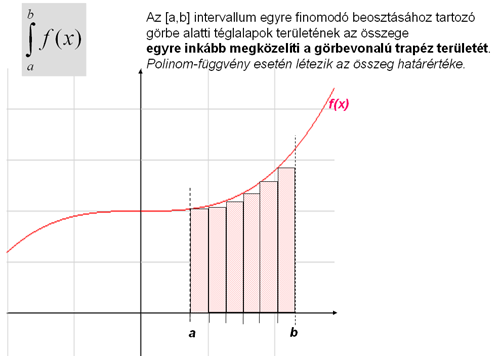
Magyarul a feladat megoldása polinomok esetén biztosan megközelíthető egy nagyon nagyszámú, n tagú összeggel (például az intervallum n egyenlő részre osztásával).

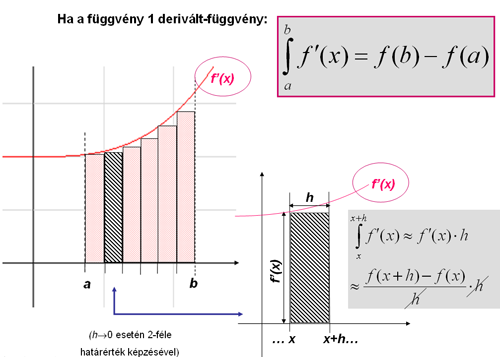
De nézzük meg, mi történik, amikor a függvény egy derivált-függvény! Azonnal hozzáteszem, hogy az eredeti függvényt éppen ismerjük, aminek a deriváltja alatti területet szeretnénk a klasszikustól eltérő módon kiszámítani. Az f'(x) alatti görbevonalú terület esete az előbbi okoskodás mentén:

Újabb határérték létezésének kö-szönhetően a kes-keny téglalapok f'(x) magassága az eredeti f(x) függ- vény x-beli differen-ciál-hányadosa a h→0 esetén. A ballonos fizika- példánkban már kijött, hogy a 0 és x idő közti út megváltozása a 0 és az x közé eső sebesség-függvény - vagyis az út derivált-függvénye - alatti területet adja.

Általánosan igaz: 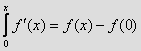Tehát az egyes téglalapok területeinek végtelen összegzése útján elérhetjük, hogy az eredeti függvény megváltozását számoljuk csak ki a 2 végpontban (az eredeti függvénybe behelyettesített felső és alsó határ értékét kiszámolva, majd kivonva egymásból):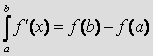

Végül láthatjuk, hogy az eredeti függvényben szereplő konstansok a különbségképzés miatt ki fognak esni. Vegyük észre, hogy a ballon esetében teljesen mindegy, hogy hány méterről engedték fel: a g(x) és h(x) függvényekben szereplő konstansok a megtett út különbség-képzése alkalmával kiesnek. 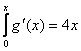illetve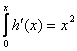
Magyarul a 4x+c és az x²+k (c, k: tetszőleges valós számok) alakú út-függvényekre ugyanaz lenne igaz, mint a választott 4x+50 és x²+20 függvényekre, mert a konstans deriváltja 0.