A fejezet nem a számonkérés részét képző anyagrésszel foglalkozik; pusztán érdekességként mutatom be.

Ha a kísérletben egyszerre két valószínűségi változónk is van, azaz két megfigyelést is végzünk egyszerre, akkor együttes eloszlástáblázatban vezetjük az együttesen bekövetkező események valószínűségeit.

Nézzünk egy példát!

32 lapos kártyapakliból húzunk 2 lapot és azt figyeljük, hogy hány az ász és hány a piros közöttük.

Írjuk fel az együttes bekövetkezések eseményeit, majd próbálkozzunk meg a valószínűségek kiszámításával!

 

16. ábra

A kísérlet: 32 lapból 2 lapot húzni egyszerre.

Legyen

X: húzott ászok száma;

Y: a húzott pirosak száma.

Ábra a 32 lap egyértelmű besorolásáról:

 

 

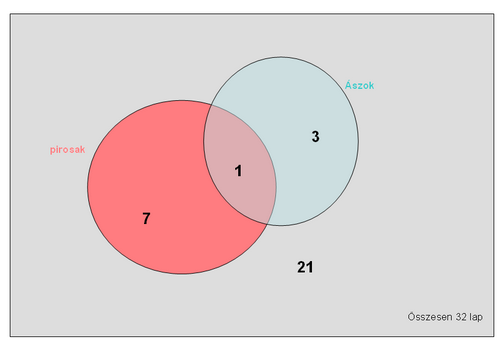
Látjuk, hogy a 32 lap között 8 a piros, 4 az ász, de 1 lap közülük a piros ász, és 21 lap se nem piros, se nem ász. Tehát 4 egymást kizáró részhalmazból választunk.

A lehetséges értékek:

X: 0,1,2

Y: 0,1,2

Ez azt jelenti, hogy egy 3x3-as táblázat celláiban megragadhatjuk X bármelyik értékét Y bármelyik értékével együtt.

Formálisan a 9 esemény elrendezése:

E_ij azt az eseményt jelenti, amikor i számú ász és j számú piros van a 2 lap között.

Ezen E események pontosítása (valószínűségek nélkül) a következő:

Innen 1 ugrás a valószínűségek beírása az urnamodell sémája segítségével...

Az összes eset: '32 alatt a 2'; n=32!/30!/2!=32*31/2 (a nevezők mindegyike)

A táblázat valóban egy eloszlástáblázat, mert az abban szereplő valószínűségek összege 1. Miért is?

Ha oszlopfolytonosan összegezzük a valószínűségeket, akkor az ászok számához tartozó valószínűségeket kapnánk, tekintet nélkül a pirosak számára. Ha pedig sorfolytonosan összegezzük a valószínűségeket, akkor a pirosak számának valószínűségeit kapnánk az ászokra való tekintet nélkül. Tehát most az X vagy az Y eloszlások vannak úgymond részletezve.

Későbbi tanulmányok során ezeket a peremeken fel is vezetjük, magyarul az utolsó sor és az utolsó oszlop után. Ekkor könnyen leellenőrizhetjük, hogy valóban az X illetve az Y valószínűségi változók eloszlását kapjuk meg az együttes valószínűségek 3x3-as mátrixának letakarásával!